前言
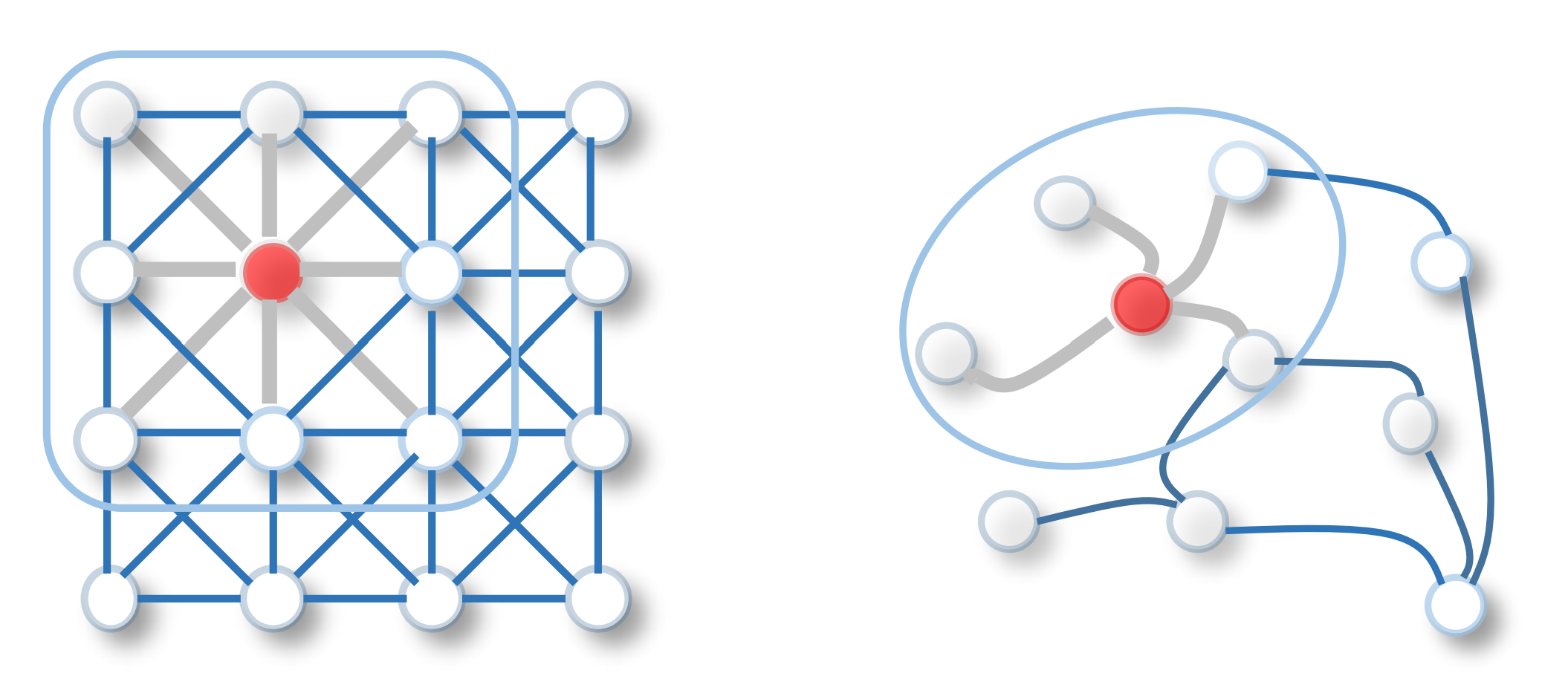左：二维欧式数据下的卷积；右：图数据下的卷积
曾经在机器学习的特征工程中主要依靠人工提取特征，而现在通过端到端的深度学习框架(CNN、RNN、自编码器)可以更好的进行特征提取。深度学习的快速发展得益于计算机算力的大幅度提升、大规模的训练数据以及可以有效的从欧式数据中提取潜在特征。虽然深度学习可以有效地应用于欧式数据，但越来越多的数据是以图的形式来表示，如：化学分子结构、论文的引文系统。图中有大小可变的无序节点，每个节点的邻居数目可能不同，导致卷积操作难以应用于图数据。且图中每个节点不再独立，节点之间通过各种类型的连接与其他节点相关。为了处理这种不规则的图数据，有了许多图数据深度学习方法的研究。现将这些图神经网络分为四类：
图循环神经网络、图卷积神经网络、图自编码器、时空图神经网络。
常用符号
研究背景
最早的图神经网络应用是1997年由Sperduti将神经网络应用于无环图，而图神经网络的概念在2005年由Gori提出。早期的研究都属于图循环神经网络，通过迭代传播邻居信息的方式来更新节点直至到达稳定，但计算量过大导致训练十分昂贵。后由于CNN在计算机视觉领域的成功，出现了大量图卷积的概念。图卷积神经网络主要分为两类，一类基于谱方法，一类基于空间方法。
GNN vs network embedding(网络嵌入表达)
network embedding旨在将网络中的节点表示为低维向量，同时保留网络拓扑结构信息与节点信息，以便使用现成工具即可轻松完成后续的图分析任务。其与GNN的主要区别在于GNN是一组为各种任务设计的神经网络模型，而network embedding涵盖了针对同一任务的各种方法，且network embedding中还包含了非深度学习的方法。
GNN vs graph kernel methods(图核方法)
graph kernel methods主要用于图分类问题，通过核函数来测量图之间的相似性，再通过支持向量机进行图监督学习。图核方法也是通过映射函数将图或节点压缩为向量，但不同于GNN图核方法的映射函数是确定的。
网络分类
- 图循环神经网络(RecGNNs)：RecGNNs通过节点不断与其邻居交换信息来更新节点信息直至到达稳定状态，RecGNNs启发了后续的研究，特别是信息传播的思想。
- 图卷积神经网络(ConvGNNs)：ConvGNNs将卷积操作从网格数据推广到图数据，主要思想为聚合自己的特征与邻居的特征来生成节点的表示。与RecGNNs不同ConvGNNs通过堆叠多个卷积层来获取节点的高级表示。
- 图自编码器(GAEs)：GAEs是一种无监督学习，通过编码器-解码器架构将节点或图编码到潜在向量空间中，并根据编码信息重建图数据。GAEs主要用于学习network embedding和图生成。
- 时空图神经网络(STGNNs)：STGNNS用于学习时空图中的信息，同时考虑空间与时间的依赖。当前许多方法使用图卷积捕获空间依赖并使用RNN或CNN捕获时间依赖。
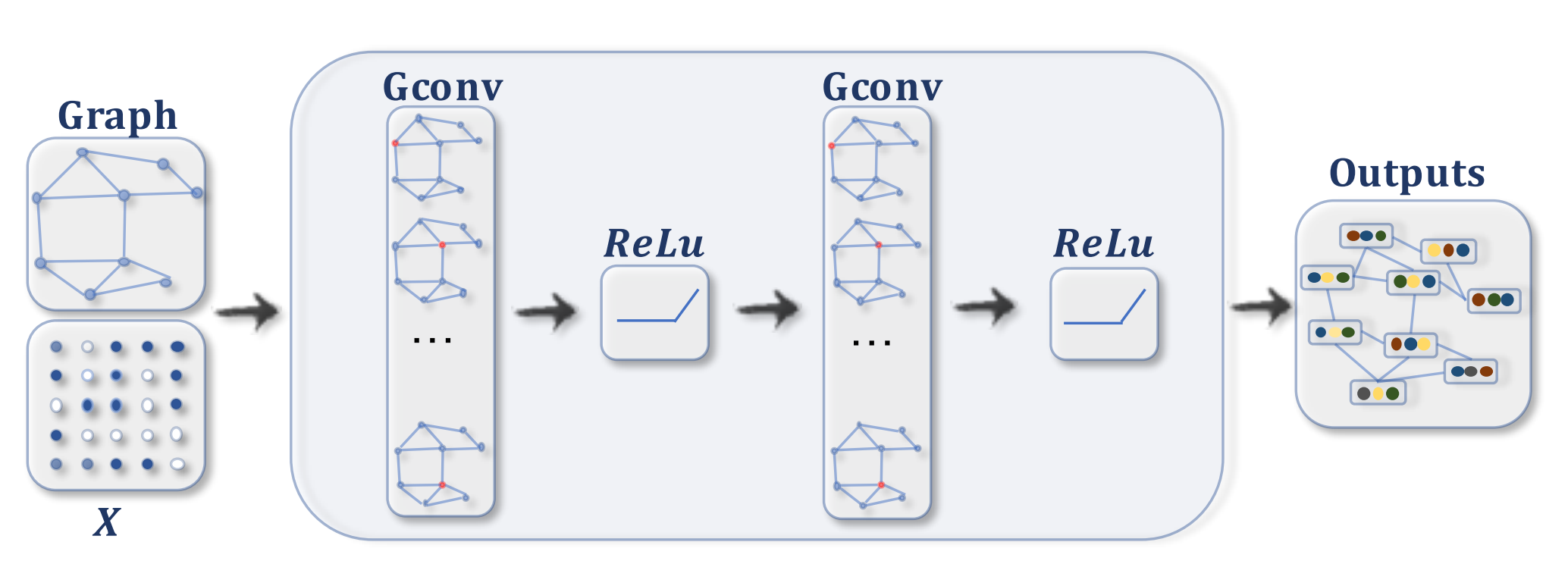ConvGNNs：具有多个图卷积层的ConvGNN，每堆叠一层卷积层，每个节点都能从更远的邻居接收消息。
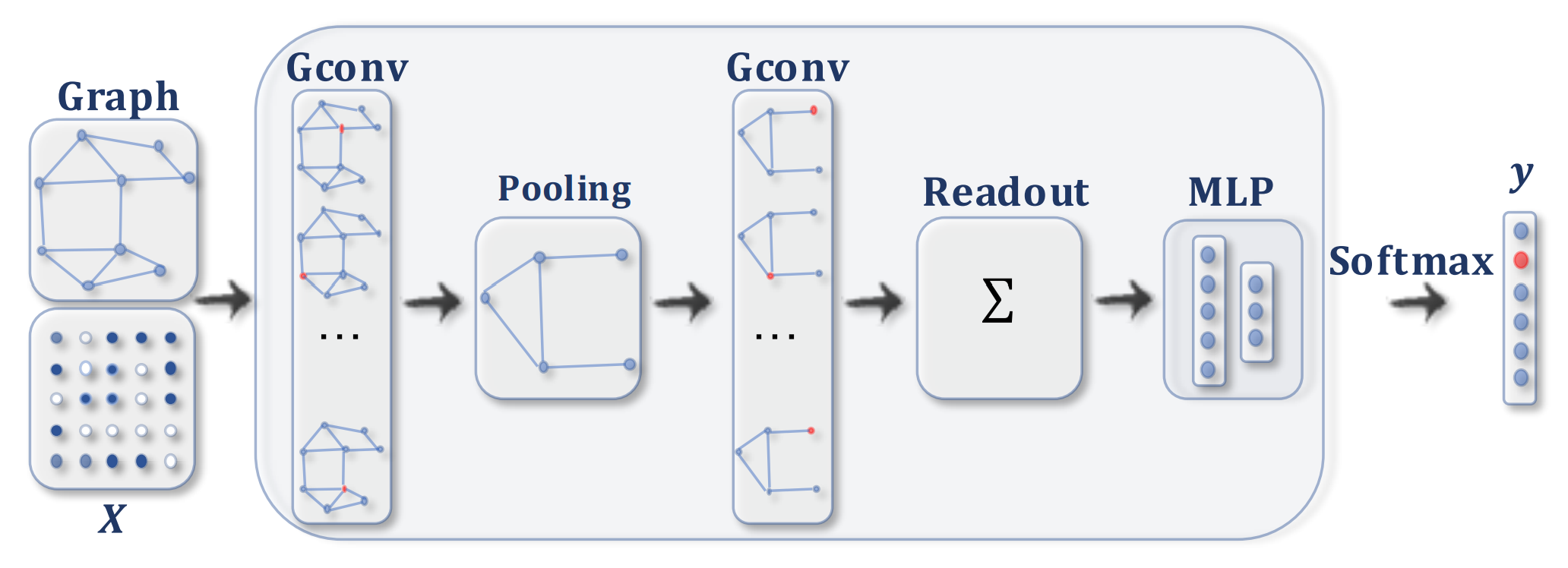ConvGNNs：用于图分类的ConvGNN，通过池化层获取粗化图，再从粗化图上的节点学习到更高级的表示，最后通过Readout层获得图的低维表示用与分类。
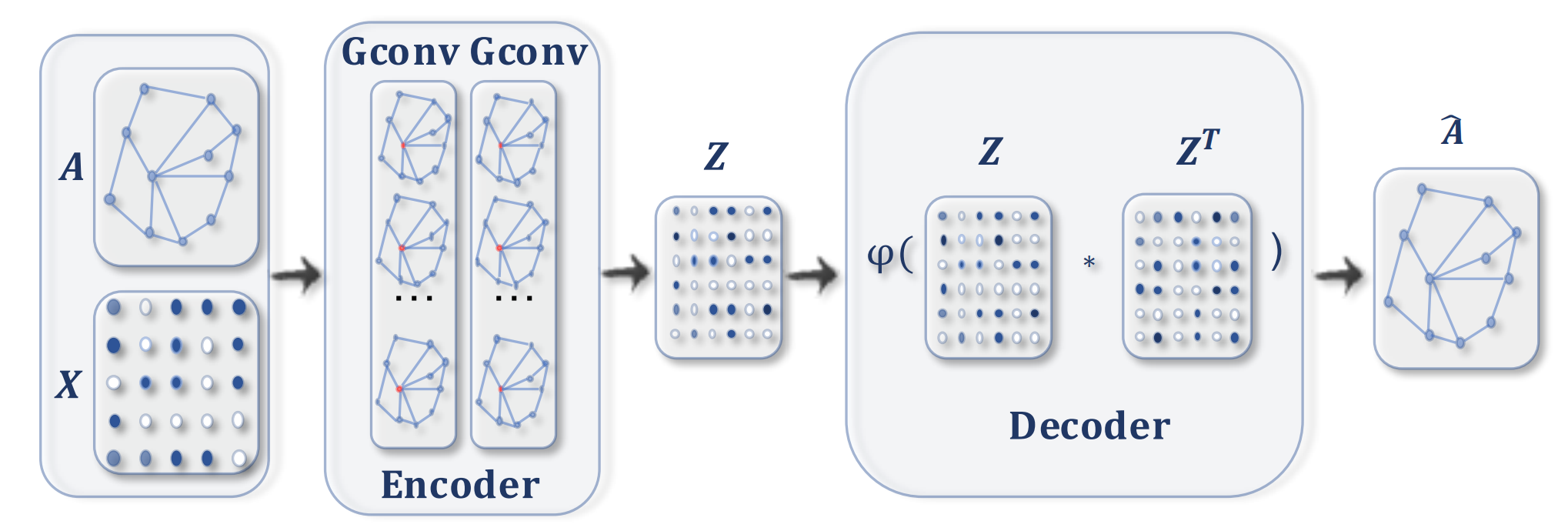GAEs：编码器使用图卷积获取每个节点的embedding，解码器计算节点embedding之间的距离重建图邻接矩阵，通过最小化原邻接矩阵与重建邻接矩阵之间的差异来训练网络。
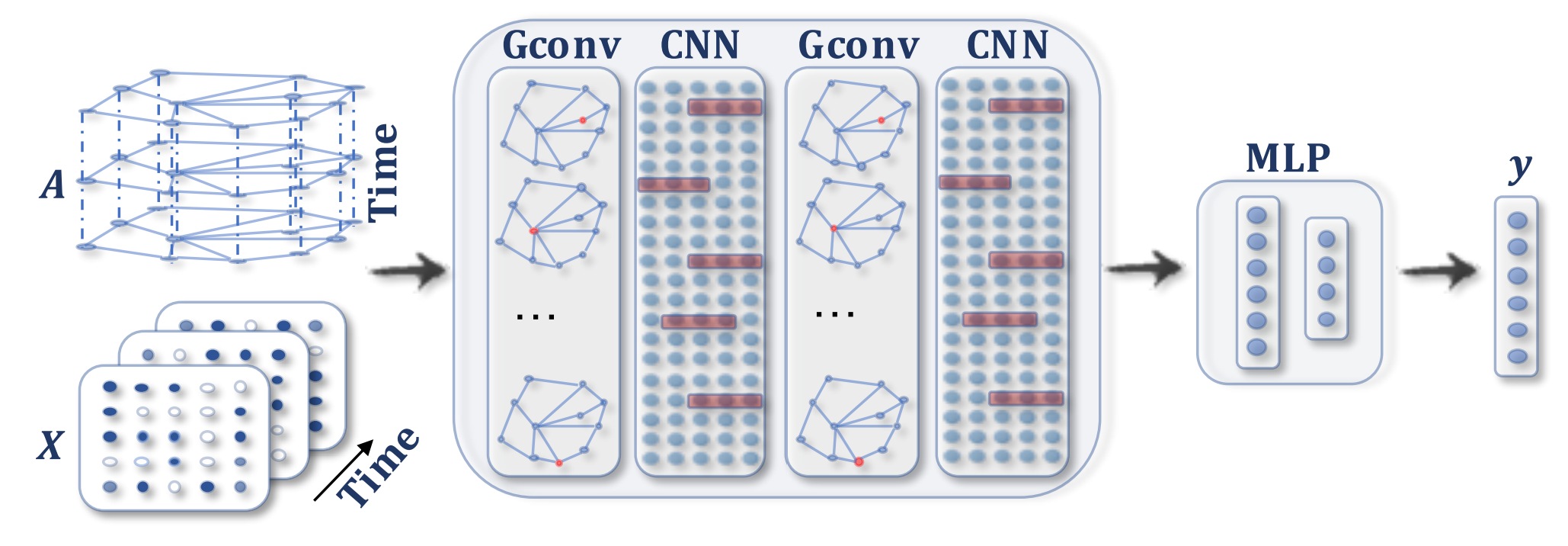STGNNs：在图卷积后加一个维CNN层，图卷积捕获空间依赖性，CNN沿时间轴滑动捕获时间依赖性。
图循环神经网络RecGNNs
图循环神经网络是GNN的先驱，它通过反复应用相同的循环层来获取节点的表示。受限于计算效率早期研究主要集中在有向无环图。
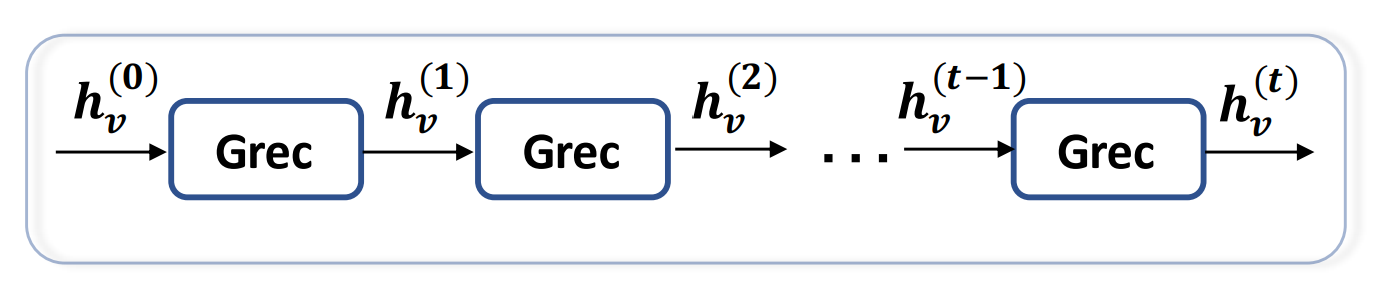RecGNNs使用相同的图循环层来更新节点
- GNN：基于信息扩散机制，通过反复交换邻居信息来更新节点信息，直到达到稳定状态，每个节点的隐藏状态都被重复更新。用求和操作来聚合邻居信息使得GNN适用于所有节点，即使邻居数量不同且不知道邻居顺序。
- GraphESN：使用echo state网络以提高模型训练效率，GraphESN由编码器和输出层组成，实现了一个收缩状态转换函数来循环更新节点状态，通过将固定节点状态作为输入来训练输出层。
- GGNN：采用门控循环单元(GRU)，将循环减少到固定的步数。节点隐藏状态由其先前的隐藏状态及其相邻的隐藏状态更新，但GGNN需要在所有节点上多次运行循环函数，且需要将所有节点的隐藏状态存储在内存中。
- SSE：提出了一种对大图的学习算法，以随机和异步的方式循环更新节点隐藏状态，交替采样一些节点用于状态更新，一些节点进行梯度计算。SSE的循环函数定义为历史状态和新状态的加权平均值。
图卷积神经网络ConvGNNs
近年来图卷积神经网络发展迅速，它通过固定数量的图卷积层来解决图循环层中相互依赖的问题。ConcGNNs分为两类，基于谱(spectral)和基于空间(spatial)的方法。基于谱的方法通过从图信号处理的角度引入滤波器来定义图卷积，其中图卷积操作被解释为从图信号中去除噪声；基于空间的方法继承了RecGNN的思想，通过信息传播来定义图卷积。
ConvGNNs使用独立的图卷积层来更新节点
基于谱的方法
谱方法在图信号处理中有坚实的数学基础。
首先假设图是无向的，归一化图拉普拉斯矩阵可用来表示无向图。拉普拉斯矩阵L如下所示：
D是度矩阵，即节点度数的对角矩阵，如下所示：
归一化图拉普拉斯矩阵是实对称且半正定的。所以归一化的拉普拉斯矩阵可以分解为：
其中U是按特征值排列的特征向量矩阵，Λ是特征值的对角矩阵。
归一化拉普拉斯矩阵的特征向量形成一个正交空间，即：
在图信号处理中，图信号x为图中节点的特征向量，对图信号x的傅里叶变换定义为：
逆图傅立叶变换定义为:
^x为图信号x经过傅里叶变换后的结果信号。图傅立叶变换将输入图信号投影到正交空间，其中基由归一化的图拉普拉斯算子的特征向量组成，变换后的信号^x是图信号在新空间中的坐标。所以输入的信号可以表示为：
这正是图傅里叶逆变换，现在输入图信号x经过滤波器g的图卷积为：
当定义：
时，谱图卷积可以简化为：
基于谱的ConvGNN都遵循上述定义，区别在于滤波器gθ的选择。
Spectral CNN：将滤波器gθ设置为一组可学习的参数，且考虑多通道的图信号。Spectral CNN的图卷积层如下式所示：
其中
由于拉普拉斯矩阵的特征分解，Spectral CNN有三点不足：
- 对图的任何扰动都会导致特征基的变化
- 学习的过滤器是仅适用于特定领域，不能应用于不同结构的图
- 特征分解需 O(n^3)的计算复杂度
ChebNet：通过特征值对角矩阵的切比雪夫多项式来近似滤波器gθ，图卷积如下所示：
再通过：
最终，ChebNet采用如下的图卷积公式：
ChebNet定义的过滤器在空间中是局部的，使得过滤器可以不受图大小的限制提取局部特征。
CayleyNet：进一步应用Cayley多项式作为参数有理复函数来捕获窄频带，卷积公式如下所示：
其中其中Re(·)返回复数的实部，c0是实系数，cj是复系数，i是虚数，h是控制Cayley滤波器频谱的参数，ChebNet是CayleyNet的一个特例。
GCN：使用了ChebNet的一阶近似，即假设K=1，λmax=2，图卷积公式如下图所示：
为了限制参数的数量并避免过拟合，进一步假设：
使得图卷积可表示为：
为了多通道输入输出，将图卷积表示为：
但根据经验，使用上述方法会使GCN的数值不稳定，所以进行如下替换：
基于空间的方法
类似于传统CNN在图像上的卷积操作，基于空间的方法根据节点的空间关系定义图卷积，将中心节点信息与其邻居的信息进行卷积，更新中心节点的信息。基于空间的ConvGNN与RecGNN具有相同的信息传播、消息传递思想。空间的图卷积操作本质上是沿边传播节点的信息。
NN4G：Neural Network for Graphs(NN4G)是与GNN在同一年提出的工作，且是第一个基于空间的ConvGNN的工作。与RecGNN不同，NN4G通过独立参数的多层神经架构来学习图的空间依赖。节点的邻域可以通过加深层数来扩展。NN4G通过如下方式来导出其下一层的节点状态：
其形式类似于GCN，但使用了未归一化的邻接矩阵，这可能会使节点的隐藏状态具有不同的尺度。
DCNN：DCNN将图卷积视为一个扩散的过程，它假设信息以一定的转移概率从一个节点转移到其相邻节点之一，这样信息分布可以在几轮后达到平衡。其图卷积定义为：
转移概率矩阵P：
在DCNN中隐藏表示矩阵H(k)与输入特征矩阵X保持相同的维度，且函数的输入不是先前的隐藏状态，最终DCNN将所有的隐藏状态连接在一起作为最后的输出。
DGC：DGC将所有对所有的进行求和而不是连接，它的图卷积式如下所示：
使用转移概率矩阵意味着远距离的邻居对中心节点的影响非常小。
PGC-DGCNN：使用最短路径增加远距离邻居参与中心邻居的信息聚合。定义了最短路矩阵S，当节点v到节点u的最短路径长度为j：
否则为0。用超参数r来控制感受野的大小。其图卷积式如下所示：
||代表对向量进行连接，但最短路径邻接矩阵的计算可能很昂贵，最大为O(n^3)
