论文pdf
前言
Purpose： 循环模型通常沿输入输出的序列顺序来计算，产生一系列的隐藏状态，通过先前的隐藏状态与当前位置的输入来输出，这种方式使得计算过程中无法并行计算。
减少顺序计算也构成了扩展模型的基础，在如ByteNet、ConvS2S等模型中关联两个输入或输出位置的信号所需的计算量随着位置的增加而增加，这使得对长序列难以建模。
Method： 注意力机制允许对依赖关系建模，无需考虑它们在输入与输出序列中的距离。作者提出了Transformer结构，用多头自注意力取代了编码器-解码器架构中的循环层，实现了一个完全基于注意力的序列转换模型。
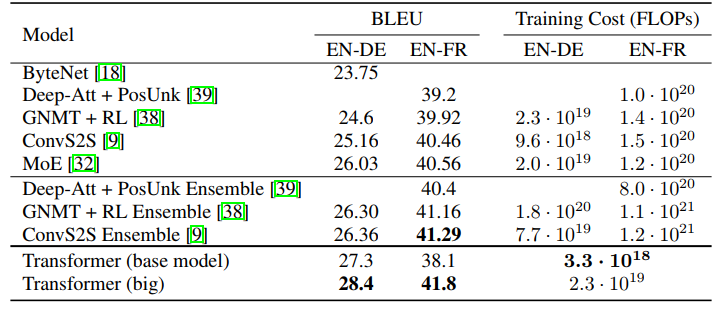
Results： 在翻译任务中因为Transformer的高并行计算，训练速度明显快于基于循环或卷积层的架构。在 WMT 2014 English-to-German 和 WMT 2014 English-to-French 翻译任务中取得了最优水平。
Architecture
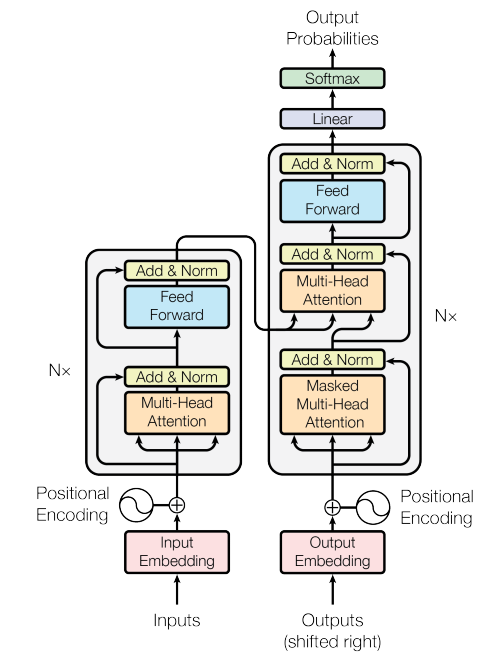
Encoder-Decoder
- Encoder：每个编码器层中均有两个子层，多头注意力(multi-head self-attention mechanism)与全连接前馈网络(Feed Forward Neural Network)。并且两个子层中均有残差连接与层归一化，即每个子层的输出为 LayerNorm(x + Sublayer(x))。因为残差连接需要相同的维度，所以模型中所有子层输出的维度为512(每个词元为一个长度为512的向量)。
- Decoder：除了编码器中的两个子层以外解码器还加入了一个encoder-decoder attention层，在这一层中Q来自解码器的输出，K、V来自编码器的输出。由于在翻译当前位置时不应该关注后续位置的信息，所以使用masked multi-head attention去掩盖住后续的输出，保证位置i的预测只依赖于位置i之前的输出，在训练与预测时的行为是一致的。解码器中同样加入了残差连接与层归一化。
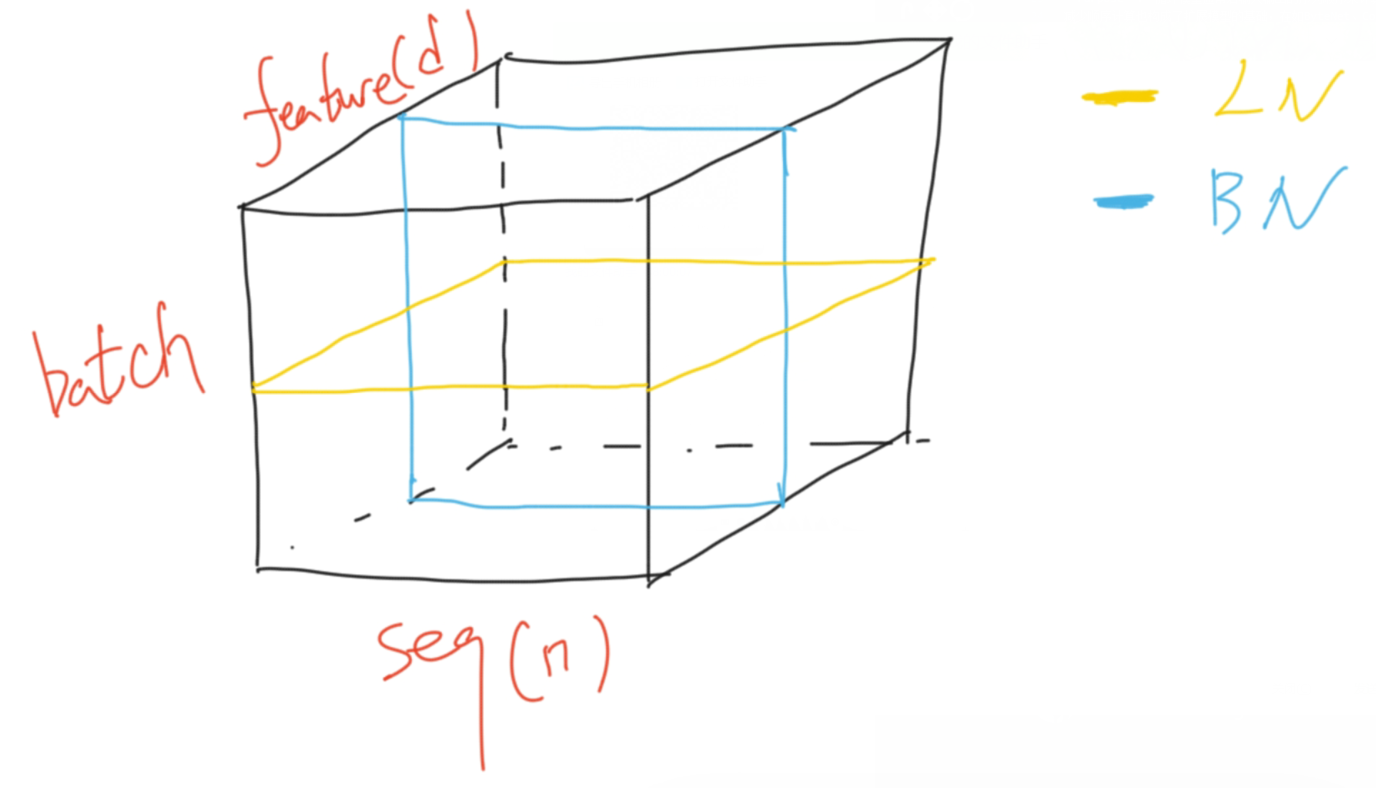
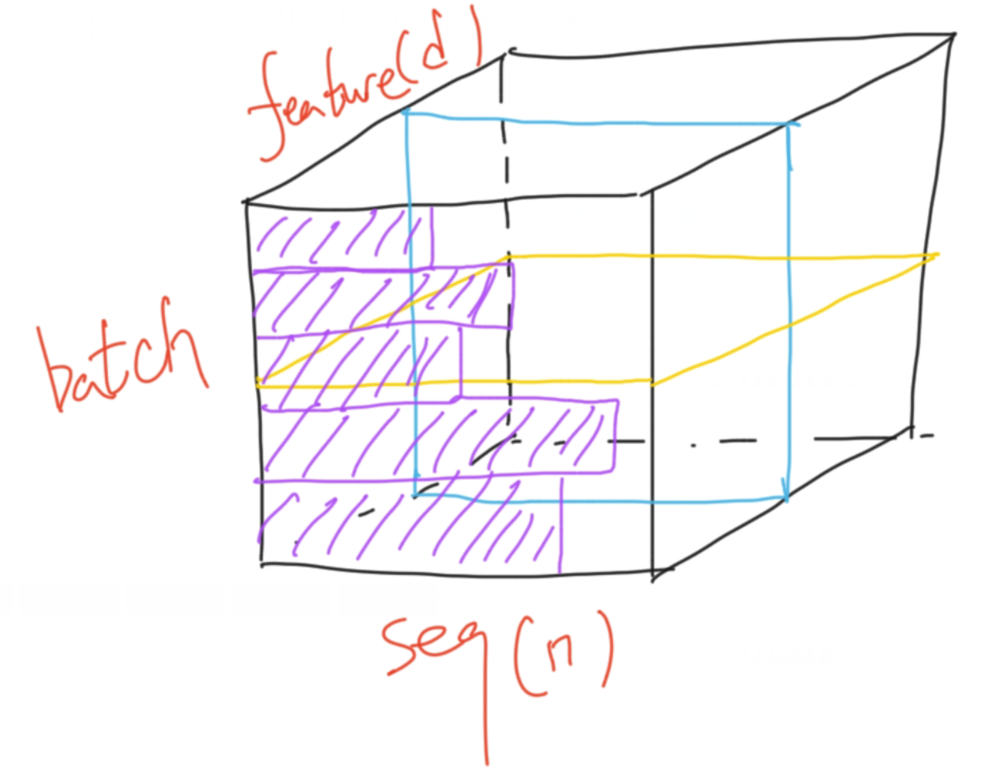
batchNorm：对同一个batch下不同样本的同一特征进行归一化；layerNorm：对同一样本的不同特征进行归一化
在机器翻译的任务中，数据的结构是如下图所示，batch的每一行为一个序列(seq)，每个序列又分为多个词元，每个词元有自己的特征也就是512维的向量。因为每个序列的长度可能不同(紫色)，小批量计算时如果序列长度变化较大，用BN算均值、方差的话抖动会比较大。而且在预测时BN要记录全局的均值、方差，则序列模型在新的预测序列如果特别长，预测偏差会较大。而LN仅计算每个序列自己的均值、方差，不论序列是长是短都会比较稳定。
Attention
self-attention：在注意力机制中有Query(Q)、Key(K)、Value(V)，attention的计算过程是计算Q与每个K的相似程度，再将相似度乘到V上得到最后的值，不同的注意力分数有不同的计算方法(如additive attention、dot-product attention)。在self-attention中Q、K、V都从输入的embedding向量中得到，长度均为64。通过三个512×64的权重矩阵学习得到，如下图所示。
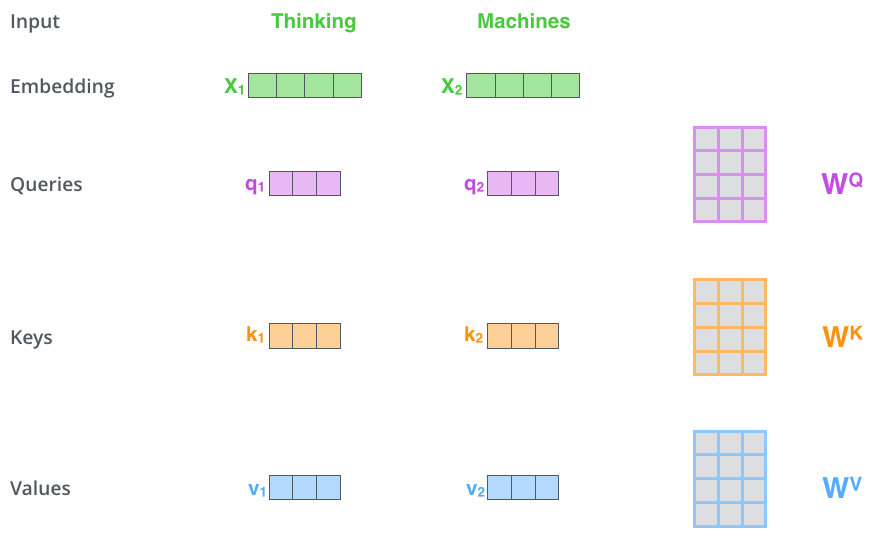attention的计算过程分为7步：
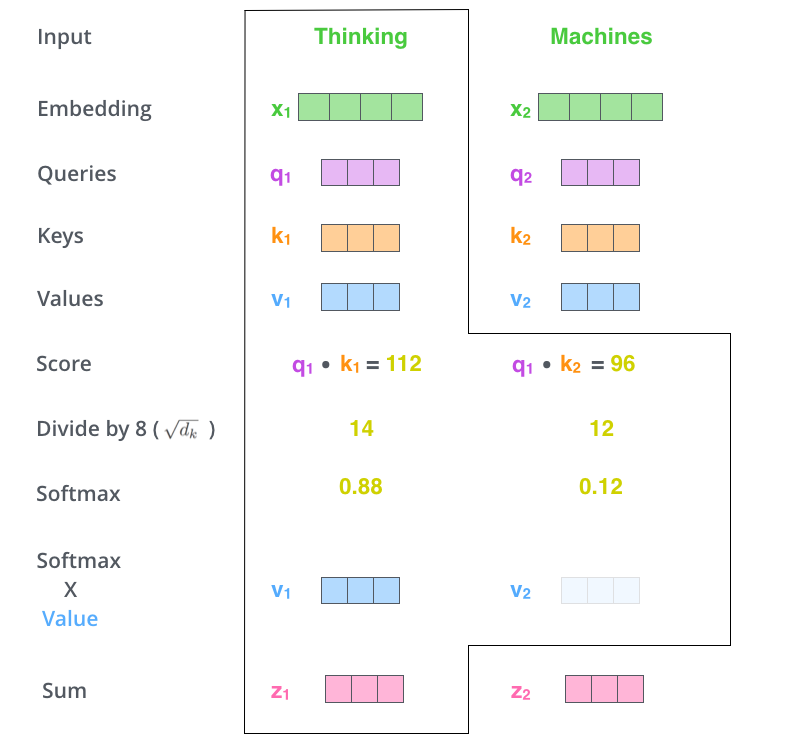
- 将输入词元转换为embedding向量。
- 由embedding向量得到Q、K、V三个向量。
- 每个词元计算一个值score=Q×K^T。
- 当Q、K向量长度较长时，点积值会过大，再经softmax函数会使梯度过小收敛变慢，所以对score进行归一化处理。
- 再进行softmax操作(矩阵计算时对每一行进行softmax操作)。
- softmax得到的值点乘V得到每个词元的评分。
- 相加得到最终输出的结果。
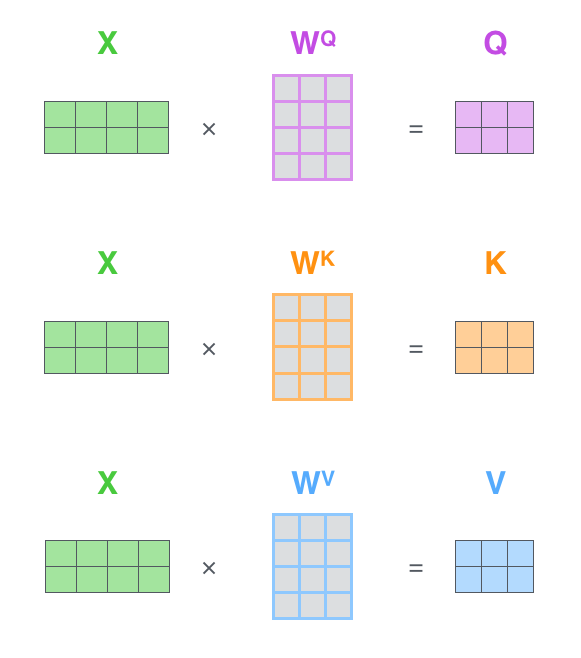
而在实际计算过程中采用矩阵计算的方式来高效计算。X中的每一行对应每一个词元。
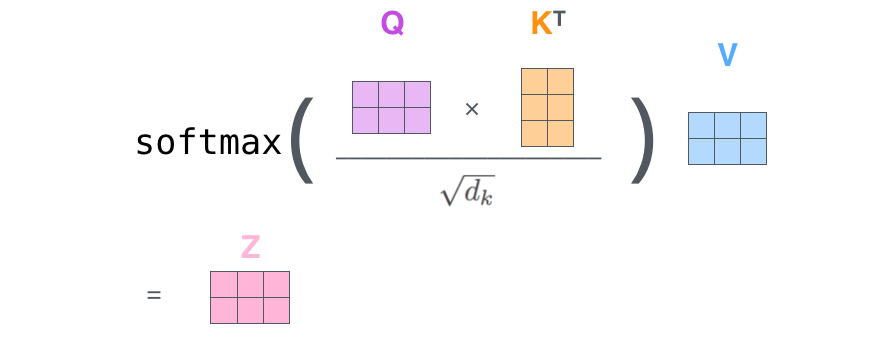
Multi-Head Attention：多头注意力相当于将每个词元进行h个不同的self-attention，再聚合到一起，对应于卷积层中的多通道输入输出。计算过程为先通过一个线性层将512维的Q、K、V降为64(512/h)维，使得总的计算量与一个单头注意力相当。再将词元向量输入到h个self-attention中得到h个特征矩阵，再将h个特征矩阵拼成一个大的特征矩阵，特征矩阵经过一层全连接层后得到最后的输出。
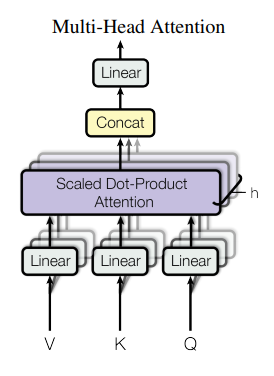
在Transformer中有三种多头注意力：
- encoder-decoder attention layers：Q来自上一个解码器的输出，K、V来自编码器的输出，这使得解码器中的每一个位置都注意了输入序列的所有位置。
- encoder layers：Q、K、V都来自相同的输入。同样使得编码器中的每一个位置都注意了编码器前一层中的所有位置。
- decoder layers：解码器中的Q、K、V应来自于它前一层的输出，但关注位置仅为当前位置之前的所有位置，通过下图中的mask操作将屏蔽的值设置为负无穷来实现。
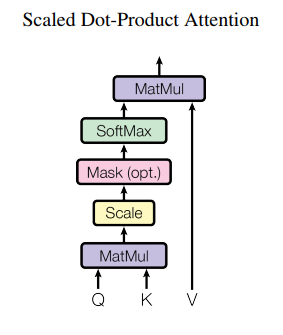
为什么用自注意力：
- 每层的计算复杂度
- 可以并行化的计算量：通过最小顺序操作数来衡量
- 网络中远距离依赖的路径长度：学习远距离的依赖时序列转换任务的关键，影响学习这种依赖关系的一个关键因素就是网络传播时需要穿越的路径长度
如下图所示，与CNN、RNN相比自注意力有更高的并行计算能力与更短的依赖路径长度，且计算复杂度不会过大。
Feed-Forward Networks
解码器和编码器中的每一层都有一个全连接的前馈网络。它通过两个1×1的卷积核进行线性变换，先将维度从512升到2048，再从2048降到512。同样有残差连接与层归一化操作。因为经过attention，也就是对输入的加权和之后，把整个序列里面的信息提取出来，汇聚到了输出中。attention的输出中已经包含了感兴趣的序列信息，所以经过FFN层映射的时候只需要对每个点进行卷积即可，1×1卷积就可以完成。
Positional Encoding
仅使用自注意力的模型中不包含时序信息，无论怎样打乱顺序都会得到同样的结果。而我们都知道句子中词出现的顺序会影响句子的意思。所以需要加入些序列信息，作者使用了位置编码(positional encodings)加入到编码器和编码器的embedding向量中，位置编码的长度与embedding向量的长度相同，直接相加即可。
pos表示词元的位置，i表示词元的维度。作者考虑到词与词之间的相对位置也很重要，所以选择如上函数使得可以很容易的计算词元间的相对位置。根据如下公式，k+p位置的向量可以表示为位置k的向量的线性变换。
